इस Class में जान पाएंगे :-
दी गई संख्या का वर्ग ज्ञात करना।
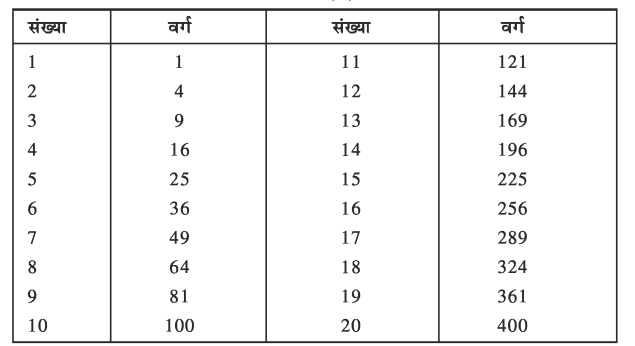
प्राकृत वर्ग संख्याओं के गुणधर्म
- जब किसी संख्या का घातांक 2 होता है, तो प्राप्त होने वाली संख्या वर्ग (Square) कहलाती हैं।
- प्रथम दस प्राकृत संख्याओं के वर्गों के इकाई के स्थान पर अंक 0, 1, 4, 5, 6 व 9 ही आते हैं।
- यदि किसी पूर्ण वर्ग संख्या के अंत में शून्यों के पूरे जोड़े बनते हैं तो वह संख्या पूर्ण वर्ग होती है।
- सम संख्याओं के वर्ग सदैव सम होते हैं। इसी प्रकार विषम संख्याओं के वर्ग सदैव विषम होते हैं।
पूर्ण वर्ग संख्याओं को ज्यामितीय वर्गों द्वारा निरूपण
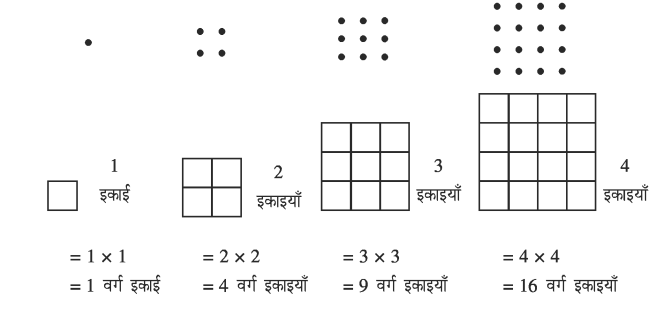
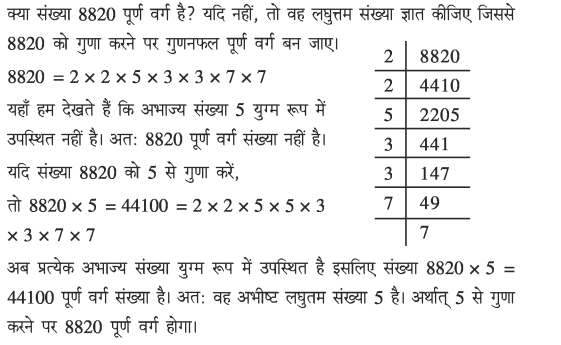
पूर्ण वर्ग की पहचान

कौन सी न्यूनतम संख्या जिसे गुणा करने पर गुणनफल पूर्ण वर्ग संख्या बन जाये ?
कौन सी न्यूनतम संख्या जिसे भाग देने पर भागफल पूर्ण वर्ग संख्या बन जाये ?
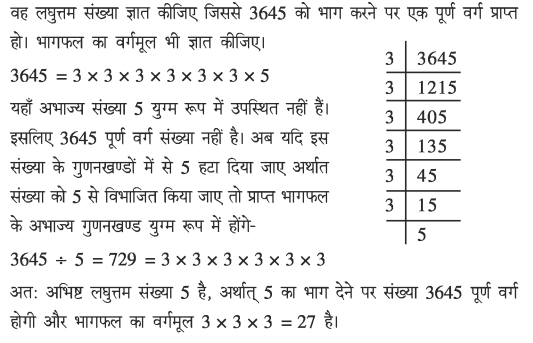
पूर्ण वर्ग संख्याओं का वर्गमूल
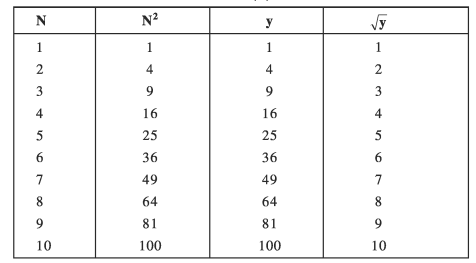
गुणनखण्ड द्वारा संख्याओं के वर्गमूल ज्ञात करना :

भाग विधि द्वारा संख्याओं के वर्गमूल ज्ञात करना :

पूर्ण घन की पहचान
अभाज्य गुणनखंड विधि:
दिए गए संख्या के अभाज्य गुणनखंड निकालें। यदि सभी गुणनखंडों की घात (power) 3 के गुणज (multiple of 3) में हो, तो वह संख्या पूर्ण घन होगी।
उदाहरण: 216 के अभाज्य गुणनखंड: 216=23×33, चूंकि सभी गुणनखंडों की घात 3 के गुणज में है, इसलिए 216 एक पूर्ण घन है।
घनमूल

20 MCQs on Numbers and Square Roots
Part 1: गुणनखण्ड और पूर्ण वर्ग
- 200 का कौन-सा गुणनखण्ड इसे पूर्ण वर्ग बनाता है?
a) 3
b) 2
c) 5
d) 7
उत्तर: b) 2 - 180 का कौन-सा गुणनखण्ड इसे पूर्ण वर्ग बनाता है?
a) 3
b) 5
c) 2
d) 7
उत्तर: b) 5 - 2352 को किस संख्या से भाग देने पर भागफल पूर्ण वर्ग बनता है?
a) 2
b) 3
c) 7
d) 5
उत्तर: b) 3 - 790 पूर्ण वर्ग क्यों नहीं है?
a) 3 का घात विषम है।
b) 7 का घात विषम है।
c) 5 और 79 का घात विषम है।
d) 2 का घात विषम है।
उत्तर: c) 5 और 79 का घात विषम है। - 16 का वर्गमूल क्या है?
a) 4
b) 8
c) 2
d) 6
उत्तर: a) 4
Part 2: पूर्ण घन पहचान
- 729 पूर्ण घन है या नहीं?
a) हाँ
b) नहीं
उत्तर: a) हाँ - 800 पूर्ण घन है या नहीं?
a) हाँ
b) नहीं
उत्तर: b) नहीं - 125 को 5 से गुणा करने पर क्या परिणाम पूर्ण घन बनेगा?
a) हाँ
b) नहीं
उत्तर: a) हाँ - 2744 का घनमूल क्या है?
a) 14
b) 12
c) 16
d) 15
उत्तर: a) 14 - 64 का घनमूल क्या है?
a) 3
b) 4
c) 6
d) 5
उत्तर: b) 4
Part 3: न्यूनतम गुणन और भाग संख्या
- 1352 को किससे गुणा करने पर पूर्ण घन बनेगा?
a) 11
b) 12
c) 13
d) 15
उत्तर: c) 13 - 8019 को किससे भाग देने पर पूर्ण घन बनेगा?
a) 3
b) 5
c) 7
d) 11
उत्तर: a) 3 - 256 को किससे गुणा करने पर यह पूर्ण घन बनेगा?
a) 2
b) 3
c) 4
d) 5
उत्तर: a) 2 - 81 का वर्गमूल क्या है?
a) 8
b) 9
c) 7
d) 6
उत्तर: b) 9 - 361 का वर्गमूल क्या है?
a) 17
b) 18
c) 19
d) 20
उत्तर: c) 19
Part 4: प्रैक्टिकल प्रश्न
- 64 को बालकों में बाँटने पर प्रत्येक बालक को उतने आम मिले जितने टोली में बालक थे। बालकों की संख्या क्या है?
a) 6
b) 8
c) 7
d) 9
उत्तर: b) 8 - 121 पूर्ण वर्ग क्यों है?
a) यह अभाज्य गुणनखंडों के जोड़े बनाता है।
b) सभी घात सम हैं।
c) इसका वर्गमूल पूर्णांक है।
d) सभी सही हैं।
उत्तर: d) सभी सही हैं। - 100 का वर्गमूल क्या है?
a) 10
b) 20
c) 25
d) 15
उत्तर: a) 10 - 196 का वर्गमूल क्या है?
a) 12
b) 13
c) 14
d) 15
उत्तर: c) 14 - अभाज्य गुणनखंडों का उपयोग किसके लिए किया जाता है?
a) वर्गमूल निकालने
b) पूर्ण वर्ग पहचानने
c) पूर्ण घन पहचानने
d) उपरोक्त सभी
उत्तर: d) उपरोक्त सभी
